¿Qué es la computación cuántica?

En 1981, Richard Feynman planteó la pregunta sobre qué tipo de computadoras se pueden usar para simular la física. Sin embargo, algunos fenómenos físicos, como la mecánica cuántica, no pueden simularse utilizando una computadora clásica. Luego, conjeturó la existencia de un modelo de computadora que se comporta bajo las reglas de la mecánica cuántica, lo que abrió un campo de investigación que ahora se llama computación cuántica.

Para comprender los conceptos básicos de la computación cuántica, es necesario recordar cómo funcionan las computadoras clásicas, y de ahí resaltar las diferencias entre estos modelos computacionales.

Miembros de la Royal Society : John Maynard Smith, Richard Feynman y Alan Turing

En 1936, Alan Turing y Emil Post describieron de forma independiente los modelos que dieron origen a la base del modelo informático conocido como la máquina Post-Turing, que describe cómo funcionan las computadoras y permitió una mayor determinación de los límites para resolver problemas.

En este modelo, las unidades de información son bits, que almacenan uno de los dos valores posibles, usualmente indicados por 0 y 1. Una máquina de computación clásica contiene un conjunto de bits y realiza operaciones que modifican los valores de los bits, también conocidos como estado. Por lo tanto, una máquina con N bits puede estar en uno de 2 ᴺ estados posibles.

Teniendo esto en cuenta, el modelo informático de Post-Turing se puede describir de forma abstracta como una máquina de estados, en la que la ejecución de un programa se traduce como transiciones de máquinas a lo largo del conjunto de estados.

Un artículo publicado por David Deutsch en 1985 describe un modelo informático que amplía las capacidades de una máquina de Turing basada en la teoría de la mecánica cuántica. Este modelo informático presenta varias ventajas sobre el modelo de Turing para procesar grandes volúmenes de información. También presenta propiedades únicas que se desvían de la forma en que entendemos la computación clásica. La mayoría de estas propiedades provienen de la naturaleza de la mecánica cuántica. Vamos a profundizar en estos detalles antes de abordar el concepto de computación cuántica.

Superposición

Una de las propiedades más interesantes de la computación cuántica que proporciona una ventaja sobre el modelo de computación clásica es la superposición. En física, la superposición es la capacidad de producir estados válidos a partir de la adición o superposición de varios otros estados que forman parte de un sistema.

Aplicando estos conceptos a la información de cómputo, significa que hay un sistema en el cual es posible generar un estado de máquina que representa una suma (ponderada) de los estados 0 y 1; en este caso, el término ponderado significa que el estado puede realizar un seguimiento de «la cantidad de» 0 y 1 presente en el estado.

En el modelo de cálculo clásico, un bit solo puede almacenar el estado de 0 o 1, no ambos; incluso utilizando dos bits, no pueden representar la suma ponderada de estos estados. Por lo tanto, para hacer una distinción de los estados básicos, la computación cuántica utiliza el concepto de bit cuántico (qubit) una unidad de información para denotar la superposición de dos estados. Este es un concepto fundamental de la computación cuántica, ya que proporciona una manera de rastrear más de un estado por unidad de información, lo que lo convierte en una herramienta poderosa para procesar información.

Computación clásica: un bit almacena solo uno de dos estados posibles: ENCENDIDO o APAGADO.

Computación cuántica: un qubit almacena una combinación de dos o más estados.

Entonces, un qubit representa la suma de dos partes: el estado 0 o 1 más la cantidad que cada estado 0/1 contribuye a producir el estado del qubit.

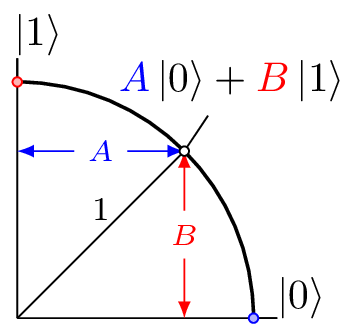
En notación matemática, qubit. | Y|Ψ es una suma explícita que indica que un qubit representa la superposición de los estados 0 y 1. Esta es la notación de Dirac utilizada para describir el valor de un qubit | Y=A | 0+B | 1|Ψ=A|0+B|1, donde, A y B son números complejos conocidos como la amplitud de los estados 0 y 1, respectivamente. El valor de los estados básicos está representado por qubits como|0=1|0+0|1|0=1|0+0|1  y |1=0|0+1|1|1=0|0+1|1, respectivamente. El lado derecho del término contiene la notación abreviada para estos estados especiales.

Medición

En una computadora clásica, los valores 0 y 1 se implementan como señales digitales. La medición de la corriente de la señal revela automáticamente el estado de un bit. Esto significa que en cualquier momento se puede observar o medir el valor del bit .

El estado de un qubit se mantiene en un sistema cerrado físicamente, lo que significa que las propiedades del sistema, como la superposición, no requieren interacción con el entorno; de lo contrario, cualquier interacción, como realizar una medición, puede causar interferencia en el estado de un qubit.

Medir un qubit es un experimento probabilístico. El resultado es un poco de información que depende del estado del qubit. La broca, obtenida por medición.| Y=A | 0+B | 1|Ψ=A|0+B|1, será igual a 0 con probabilidad |A|2|A|2, e igual a 1 con probabilidad |B|2|B|2, dónde |x||x|representa el valor absoluto dexx.

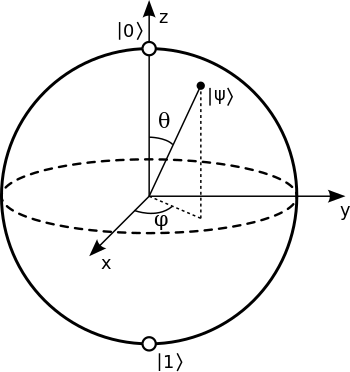
De las estadísticas, sabemos que la suma de las probabilidades de todos los eventos posibles es siempre igual a 1, por lo que debe sostener que | Un | 2 + | B | 2 =1|A|2+|B|2=1. Esta última ecuación motiva a representar qubits como los puntos de un círculo de radio uno, y más generalmente, como los puntos en la superficie de una esfera de radio uno, que se conoce como la esfera de Bloch .

El estado qubit es análogo a un punto en un círculo unitario.

The Bloch Sphere de Smite-Meister – Trabajo propio, CC BY-SA 3.0.

Vamos a desglosarlo: si mide un qubit, también destruye la superposición del qubit, lo que resulta en un colapso del estado de superposición, donde asume uno de los estados básicos, proporcionando su resultado final.

Otra forma de pensar acerca de la superposición y la medición es a través del experimento de lanzar monedas.

Lance una moneda en el aire y dé a las personas una opción aleatoria entre dos opciones: cara o cola. Ahora, no se centre en la aleatoriedad del experimento, en vez de eso, tenga en cuenta que mientras la moneda gira en el aire, los participantes no están seguros de qué lado estará boca arriba cuando la moneda caiga. Por el contrario, una vez que la moneda se detiene con una cara aleatoria hacia arriba, los participantes están 100% seguros del estado.

¿Cómo se relaciona? Los Qubits son similares a los participantes. Cuando un qubit está en una superposición de estados, está rastreando la probabilidad de caras o colas, que es el cociente de incertidumbre de los participantes mientras la moneda está en el aire. Sin embargo, una vez que comience a medir el qubit para recuperar su valor, la superposición desaparecerá y un valor de bit clásico se quedará: cabezas o colas. La medición es ese momento en el que la moneda es estática con un solo lado hacia arriba.

Una moneda justa es una moneda que no está sesgada. Cada lado (suponiendo que 0 = caras y 1 = colas) de una moneda normal tiene la misma probabilidad de adherirse después de realizar una medición. El qubit1√2|0+1√2|112|0+12|1Describe las probabilidades de lanzar una moneda justa. Tenga en cuenta que cuadrar cualquiera de las amplitudes da como resultado 1/2, lo que indica que hay un 50% de probabilidad de que las cabezas o las colas se peguen.

Sería interesante poder cargar una moneda justa a voluntad mientras esté en el aire. Aunque esta es la magia de un ilusionista profesional, esta tarea, de hecho, puede lograrse realizando operaciones sobre qubits. Entonces, prepárate para convertirte en el próximo mago cuántico.

Puertas cuánticas

Una compuerta lógica representa una función booleana que opera sobre un conjunto de entradas (a la izquierda) y que produce una salida (a la derecha). Un circuito lógico es un conjunto de compuertas lógicas conectadas, una forma conveniente de representar operaciones de bit.

La puerta NOT es una operación de un solo bit que cambia el valor del bit de entrada.

Otras puertas son AND, OR, XOR y NAND, y más. Un conjunto de puertas es universal si puede generar otras puertas. Por ejemplo, las puertas NOR y NAND son universales, ya que cualquier circuito puede construirse utilizando solo estas puertas.

La computación cuántica también admite una descripción utilizando circuitos. Las puertas cuánticas operan sobre qubits, modificando la superposición de los estados. Por ejemplo, hay una puerta cuántica análoga a la puerta NO, la puerta X.

La puerta cuántica X intercambia las amplitudes de los estados del qubit de entrada.

La puerta cuántica Z cambia la amplitud del estado 1 del signo:

Otra puerta cuántica es la puerta de Hadamard, que genera una superposición equiprobable de los estados básicos.

Usando nuestra analogía con lanzar monedas, la puerta Hadamard tiene la acción de lanzar una moneda justa al aire. En los circuitos cuánticos, un triángulo representa la medición de un qubit, y el bit resultante se indica mediante un cable doble.

Otras puertas, como la puerta CNOT, las puertas de Pauli, la puerta Toffoli, la puerta Deutsch, son ligeramente más avanzadas. Quirk , el patio de juegos de código abierto, es un arenero divertido donde puedes construir circuitos cuánticos usando todas estas puertas.

Reversibilidad

Una operación es reversible si existe otra operación que hace retroceder el estado de salida al estado inicial. Por ejemplo, una puerta NO es reversible ya que la aplicación de una segunda puerta NO recupera la entrada inicial.

En contraste, Y, O, las puertas NAND no son reversibles. Esto significa que algunos cálculos clásicos no pueden ser revertidos por un circuito clásico que usa solo los bits de salida. Sin embargo, si inserta bits de información adicionales, la operación puede revertirse.

La computación cuántica se centra principalmente en los cálculos reversibles, porque siempre hay una manera de construir un circuito reversible para realizar un cálculo irreversible. La versión reversible de un circuito podría requerir el uso de auxiliares qubits como variables auxiliares (pero no de carácter temporal).

Debido a la naturaleza de los sistemas compuestos, podría ser posible que estas ancillas (qubits extra) se correlacionen con qubits del cómputo principal. Esta correlación hace que sea imposible reutilizar las ancillas, ya que cualquier modificación podría tener un efecto secundario en el funcionamiento de un circuito reversible. Esto es como la memoria asignada a un proceso por el sistema operativo: el proceso no puede usar la memoria de otros procesos o podría causar daños en la memoria, y los procesos no pueden liberar su memoria asignada a otros procesos. Puede usar mecanismos de recolección de basura para ancillas, pero realizar cálculos reversibles aumenta su presupuesto de qubit.

Sistemas compuestos

En mecánica cuántica, un solo qubit puede describirse como un único sistema cerrado: un sistema que no tiene interacción con el entorno ni con otros qubits. Dejar que los qubits interactúen con otros conduce a un sistema compuesto donde se representan más estados. El estado de un sistema compuesto de 2 qubitos se denota comoA 0 | 00+ A 1 | 01+ A 2 | 10+ A 3 | 11A0|00+A1|01+A2|10+A3|11, dónde, A iAyo los valores corresponden a las amplitudes de los cuatro estados básicos 00, 01, 10 y 11. Este qubit 12|00+12|01+12|10+12|1112|00+12|01+12|10+12|11 representa la superposición de estos estados básicos, teniendo ambos la misma probabilidad obtenida después de medir los dos qubits.

En el caso clásico, el estado de N bits representa solo uno de los 2ᴺ estados posibles, mientras que un estado compuesto de N qubits representa todoslos estados 2ᴺ pero en superposición. Esta es una gran diferencia entre estos modelos de computación, ya que posee dos propiedades importantes: el entrelazamiento y el paralelismo cuántico.

Enredo

De acuerdo con la teoría detrás de la mecánica cuántica, algunos estados compuestos pueden describirse a través de la descripción de sus constituyentes. Sin embargo, hay estados compuestos en los que no es posible una descripción, conocidos como estados entrelazados .

Los estados de campana son ejemplos de qubit enredados.

El fenómeno del enredo fue señalado por Einstein, Podolsky y Rosen en la llamada paradoja de EPR . Supongamos que hay un sistema compuesto de dos qubits enredados, en el que al realizar una medición en un qubit se causa una interferencia en la medición del segundo. Esta interferencia ocurre incluso cuando los qubits están separados por una larga distancia, lo que significa que parte de la transferencia de información ocurre más rápido que la velocidad de la luz. Así es como el entrelazamiento cuántico entra en conflicto con la teoría de la relatividad, donde la información no puede viajar más rápido que la velocidad de la luz. La paradoja de EPR motivó una mayor investigación para derivar nuevas interpretaciones sobre la mecánica cuántica y el objetivo de resolver la paradoja.

El entrelazamiento cuántico puede ayudar a transferir información a distancia siguiendo un protocolo de comunicación. Los siguientes ejemplos de protocolo se basan en el hecho de que Alice y Bob poseen por separado uno de los dos qubits enredados:

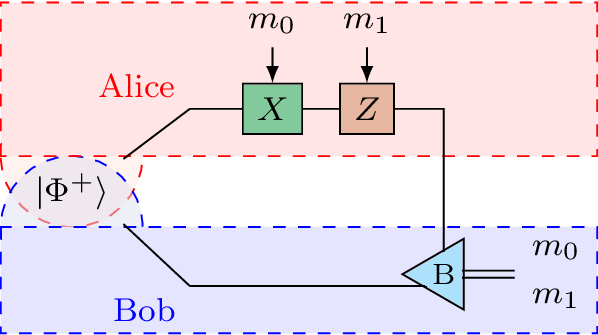
El protocolo de codificación superdense permite a Alice comunicar un mensaje de 2 bits. m 0 , m 1metro0,metro1Bob utilizando un canal de comunicación cuántica, por ejemplo, utilizando fibra óptica para transmitir fotones. Todo lo que Alice tiene que hacer es operar en su qubit de acuerdo con el valor del mensaje y enviar el qubit resultante a Bob. Una vez que Bob recibe el qubit, mide ambos qubits, observando que el estado de 2 bits colapsado corresponde al mensaje de Alice.

Protocolo de codificación superdense.

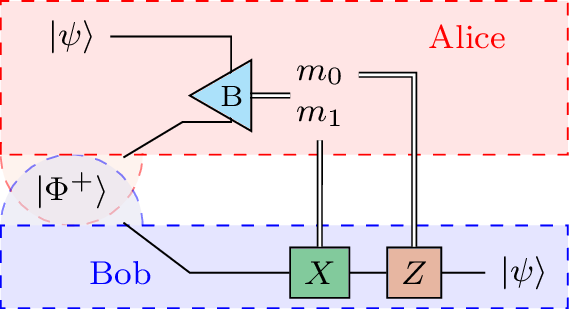
El protocolo de teletransportación cuántica le permite a Alice transmitir un qubit a Bob sin utilizar un canal de comunicación cuántica. Alice mide el qubit para enviar a Bob y su qubit enredado dando como resultado dos bits. Alice envía estos bits a Bob, quien opera en su qubit enredado de acuerdo con los bits recibidos y observa que el estado del resultado coincide con el estado original del qubit de Alice.

Protocolo de teletransportación cuántica.

Paralelismo cuántico

Los sistemas compuestos de qubits permiten la representación de más información por estado compuesto. Tenga en cuenta que operar en un estado compuesto de N qubits es equivalente a operar sobre un conjunto de 2ᴺ estados en superposición. Este procedimiento es el paralelismo cuántico .En esta configuración, operar sobre un gran volumen de información da la intuición de realizar operaciones en paralelo, como en el paradigma de computación paralela; Una gran advertencia es que la superposición no es equivalente al paralelismo.

Recuerde que un estado compuesto es una superposición de varios estados, por lo que un cálculo que toma un estado compuesto de entradas dará como resultado un estado compuesto de salidas. La principal divergencia entre el paralelismo clásico y el cuántico es que el paralelismo cuántico puede obtener solo uno de los resultados procesados. Observe que una medición en la salida de un estado compuesto hace que los qubits se colapsen solo en una de las salidas, haciendo que sea imposible calcular todos los valores calculados.

Aunque el paralelismo cuántico no coincide precisamente con la noción tradicional de computación paralela, aún puede aprovechar esta potencia de cálculo para obtener información relacionada.

Problema de Deutsch-Jozsa : SupongamosFFes una función que toma como entrada N bits, genera un bit, y es constante (siempre genera el mismo valor para todas las entradas) o balanceada (genera 0 para la mitad de las entradas y 1 para la otra mitad). El problema es determinar siFF Es constante o equilibrado.

El algoritmo cuántico que resuelve el problema de Deutsch-Jozsa utiliza el paralelismo cuántico. Primero, los N qubits se inicializan en una superposición de 2ᴺ estados. Luego, en un solo disparo, se evalúa.FF para todos estos estados

(note que algunos factores fueron omitidos por simplicidad)

El resultado de aplicar FFAparece (en el exponente) de la amplitud del estado todo-cero. Tenga en cuenta que sólo cuandoFFes constante es esta amplitud, ya sea +1 o -1. Si el resultado de la medición del N qubit es una cadena de bits de todos ceros, entonces hay un 100% de certeza de queFFes constante Cualquier otro resultado indica queFF es equilibrado

Un algoritmo clásico determinista resuelve este problema utilizando 2 N – 1 +12norte−1+1 evaluaciones de FFEn el peor de los casos. Mientras tanto, el algoritmo cuántico requiere solo una evaluación. El problema de Deutsch-Jozsa ejemplifica la ventaja exponencial de un algoritmo cuántico sobre los algoritmos clásicos.

Computadoras cuánticas

La teoría de la computación cuántica está respaldada por investigaciones en el campo de la mecánica cuántica. Sin embargo, la construcción de una máquina cuántica requiere un sistema físico que permita representar los qubits y la manipulación de estados de una manera confiable y precisa.

Los Criterios DiVincenzo requieren que una implementación física de una computadora cuántica debe:

Ser escalable y tener qubits bien definidos.

Ser capaz de inicializar qubits a un estado.

Tener largos tiempos de decoherencia para aplicar códigos de corrección de errores cuánticos. La decoherencia de un qubit ocurre cuando el qubit interactúa con el entorno, por ejemplo, cuando se realiza una medición.

Utilice un conjunto universal de puertas cuánticas.

Ser capaz de medir qubits individuales sin modificar otros.
Las implementaciones físicas de computadores cuánticos enfrentan enormes obstáculos de ingeniería para satisfacer estos requisitos. El desafío más importante es garantizar tasas de error bajas durante el cálculo y la medición. La reducción de estas tasas requiere técnicas para la corrección de errores, que agregan un número significativo de qubits especializados en esta tarea. Por esta razón, el número de qubits de una computadora cuántica no debe considerarse como para los sistemas clásicos. En una computadora clásica, todos los bits de una computadora son efectivos para realizar un cálculo, mientras que el número de qubits es la suma de los qubits efectivos (aquellos que se usan para hacer cálculos) más las ancillas (usadas para cálculos reversibles) más la corrección de errores qubits

Las implementaciones actuales de las computadoras cuánticas satisfacen parcialmente los criterios de DiVincenzo. Las computadoras adiabáticas cuánticas encajan en esta categoría ya que no funcionan con puertas cuánticas. Por esta razón, no se consideran computadoras cuánticas universales.

Computadoras adiabáticas cuánticas

Un problema recurrente en la optimización es encontrar el mínimo global de una función objetivo. Por ejemplo, un sistema de control de tráfico de ruta se puede modelar como una función que reduce el costo de enrutamiento al mínimo. El recocido simulado es un procedimiento heurístico que proporciona una buena solución para este tipo de problemas. El recocido simulado encuentra el estado de la solución introduciendo lentamente cambios ( el proceso adiabático ) en las variables que gobiernan el sistema.

El recocido cuántico es la versión cuántica análoga del recocido simulado. Un qubit se inicializa en una superposición de estados que representan todas las soluciones posibles al problema. Aquí se utiliza el operador hamiltoniano, que es la suma de los vectores de las energías potenciales y cinéticas del sistema. Por lo tanto, la función objetivo se codifica utilizando este operador que describe la evolución del sistema en correspondencia con el tiempo. Luego, si se permite que el sistema evolucione muy lentamente, eventualmente aterrizará en un estado final que representa el valor óptimo de la función objetivo.

Actualmente, existen computadoras adiabáticas en el mercado, como los sistemas D-Wave e IBM Q, con cientos de qubits; sin embargo, sus capacidades están limitadas en cierta medida a algunos problemas que pueden modelarse como problemas de optimización. Van Dam et alestudiaron los límites de las computadoras adiabáticas , lo que demuestra que a pesar de resolver problemas de búsqueda local e incluso algunos casos del problema de SAT máximo , existen problemas de búsqueda más difíciles que este modelo de computación no puede resolver de manera eficiente.

Resonancia magnética nuclear

La resonancia magnética nuclear (RMN) es un fenómeno físico que se puede usar para representar qubits. El giro del núcleo atómico de las moléculas se ve perturbado por un campo magnético oscilante. Un informe de 2001 describe la implementación exitosa del algoritmo de Shor en una computadora cuántica de RMN de 7 qubits. Un resultado icónico ya que esta computadora fue capaz de factorizar el número 15.

Nucleus spinning inducido por un campo magnético, Darekk2 – CC BY-SA 3.0

Espectrómetro NRM por UCSB

Superconductoras computadoras cuánticas

Una forma de construir físicamente los qubits se basa en superconductores, materiales que conducen la corriente eléctrica con resistencia cero cuando se exponen a temperaturas cercanas al cero absoluto.

El efecto Josephson, en el que la corriente fluye a través de la unión de dos superconductores separados por un material no superconductor, se utiliza para implementar físicamente una superposición de estados.

Un cruce de Josephson – Dominio público

Cuando se aplica un flujo magnético a esta unión, la corriente fluye continuamente en una dirección. Pero, dependiendo de la cantidad de flujo magnético aplicado, la corriente también puede fluir en la dirección opuesta. Existe una superposición cuántica de corrientes que van tanto en el sentido de las agujas del reloj como en el sentido contrario a las agujas del reloj, lo que lleva a una implementación física de un qubit llamado flujo qubit . El dispositivo completo se conoce como el dispositivo superconductor de interferencia cuántica (SQUID) y se puede acoplar fácilmente escalando el número de qubits. Por lo tanto, los SQUID son como los transistores de una computadora cuántica.

SQUID: Dispositivo superconductor de interferencia cuántica. Imagen de Kurzweil Network y fuente original .

Ejemplos de computadoras superconductoras son:

Las computadoras adiabáticas de D-wave procesan el recocido cuántico para resolver diversos problemas de optimización.

La computadora de 72 qubits de Google se anunció recientemente y también varios problemas de ingeniería , como el logro de temperaturas más bajas.

IBM -Q IBM de IBM , una computadora adiabática de 20 qubit, e IBM Q Experience, un sistema basado en la nube para explorar circuitos cuánticos.

Sistema de enfriamiento D-Wave de D-Wave Systems Inc.

IBM Q System

IBM Q System One criostato en el CES.

La amenaza inminente de los algoritmos cuánticos